
Aetherometry and Gravity: An Introduction
by David Pratt
April 2005
This article presents a brief outline of the aetherometric theory of gravity and antigravity, based on Volume 1 and Volume 2A of Experimental Aetherometry, the first six monographs of The Gravitational Aether, and additional discussion in the ISFA Aetherometry Study Group.
Contents
1. Electroscopes and antigravity
2. Mass-to-length transformation
3. Gravitational pendulums
4. Cycloids and gravity
5. Mass-energy and gravitons
6. Aether flux and celestial motions
7. Inertia and Newton's first law
8. Centrifugal force and Newton's third law
9. Gravity and antigravity
10. Correas vs. Spolter
11. Closing thoughts
1. Electroscopes and antigravity
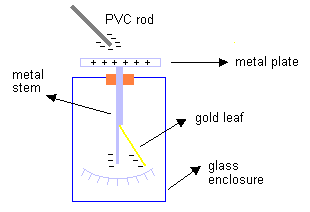 Physicists commonly regard the electroscope
as a simple, well-understood instrument. But as Paulo and Alexandra Correa
demonstrate in the first monograph of Experimental Aetherometry, the
device is 'one of the most provocative and poorly understood instruments
available to us in basic natural research'. Once the electroscope is charged,
the gold leaf lifts away from the stem as a result of electrostatic repulsion.
The length of time the leaf remains deflected is usually said to depend on
ambient conditions, such as temperature, pressure, and humidity, and in
particular the presence of ions and/or ionizing electromagnetic radiation, which
cause the charge in the stem and leaf to leak away.
Physicists commonly regard the electroscope
as a simple, well-understood instrument. But as Paulo and Alexandra Correa
demonstrate in the first monograph of Experimental Aetherometry, the
device is 'one of the most provocative and poorly understood instruments
available to us in basic natural research'. Once the electroscope is charged,
the gold leaf lifts away from the stem as a result of electrostatic repulsion.
The length of time the leaf remains deflected is usually said to depend on
ambient conditions, such as temperature, pressure, and humidity, and in
particular the presence of ions and/or ionizing electromagnetic radiation, which
cause the charge in the stem and leaf to leak away.
The conventional view is that if the electroscope were placed in a perfect vacuum - even in the presence of a gravitational field - the leaf would remain deflected indefinitely! This irrational belief in a stationary force that performs no work, not even against gravity, highlights what the Correas see as the need to go back to the bench, to very basic science, and correct fundamental misconceptions.
Everyone agrees that when the gold leaf is initially repelled by the stem it has to do work against gravity. Thereafter, because the leaf seems to be essentially stationary at the macroscopic level, orthodox physics maintains that it does not have to perform any further antigravitational work, no matter how long it stays deflected. Rejecting this 'implicit and underhanded recourse to perpetual motion' by classical electrostatic theory, the Correas argue that, in the presence of a gravitational field, the leaf can only remain deflected for as long as the kinetic energy it expends in doing work against gravity can be replenished in some way.
They point out that simple observation or sense perception validates this reasoning: a rigid statue with an arm held out horizontally, parallel to the Earth's surface, will eventually develop cracks, most likely at the joint of the arm with the body. They advise mechanistically minded scientists to try the experiment themselves and to hold out their arms horizontally for as long as they can, so that they get a sense of what it means to expend energy to resist the force of gravity.
On the basis of their experimental results with electroscopes and the theory of gravity they have developed by building on Wilhelm Reich's work with the gravitational pendulum (see below), the Correas show that, depending on ambient factors, the total kinetic energy expended by the trapped charges in opposing gravity can be hundreds of times greater than the input electric energy employed to charge the electroscope. They conclude that 'electrostatic' repulsion is actually an electrodynamic phenomenon in which the kinetic energy which repelling charge lattices spend in doing antigravitational work has to be regenerated by some form of radiant energy contributed by the local environment. Realistically, no forces can be sustained without energy expenditure, energy flow or energy transfer. A force without energy flow is a blank abstraction.
Further electroscopic anomalies are explored in depth in subsequent monographs of Experimental Aetherometry. As Eugene Mallove once said, 'the monographs unfold like a detective story'. Anomalies that conventional physics is totally unable to explain include the following:
- if the Sun were predominantly a source of ionizing radiation, the rate of leakage in an electroscope placed outdoors should be very slow in the early morning, speed up at noon or thereafter as the Sun reaches zenith, and slow down towards nightfall - instead one observes the exact opposite;
- blackbody electromagnetic radiation with a wavelength greater than 300 nanometres arrests or slows down the discharge rate of an electroscope, instead of accelerating it, as conventional physics predicts (no one seems to have even noticed this extraordinary fact before the Correas!);
- there is a constant positive temperature difference between the space at the top of the inner metallic layer of an orgone accumulator (ORAC) and the surrounding atmosphere (an ORAC is essentially a metal cage surrounded by alternating layers of conductors and insulators);
- both negatively and positively charged electroscopes discharge more slowly inside an ORAC than outside one.
Through meticulous and methodical experimentation with electroscopes, ORACs, and Tesla coils, the Correas have succeeded in identifying different types of massfree (or aetheric) energy and in explaining all the above anomalies. They have also developed several patented technologies that tap aether energy. The aether component whose action they have identified as being chiefly responsible for what they call the electroscopic 'gravito-kinetoregenerative phenomenon' is a nonelectric form of massfree energy with antigravitic properties; it is associated with the molecules of matter and their phase states, and is loosely known to chemists and meteorologists as 'latent heat'.
The other major aether component (whose spectrum the Correas have identified) is massfree electric energy consisting of longitudinal wave radiation that carries ambipolar rather than monopolar charges, for, in contrast to massbound charges (such as electrons and protons), massfree charges are neutral rather than either positive or negative. As for electromagnetic radiation, photons are considered to be transient, vortex-like standing waves in the aether, which are generated locally when particles of matter decelerate and shed the kinetic energy gained from interaction with massfree electric radiation. The aether is therefore not to be confused with the electromagnetic 'zero-point field'.
Aetherometry proposes that when units of nonelectric aether superimpose and condense to form matter particles (mass-energy), each massbound particle is accompanied by a quantum of massfree gravitational energy (i.e. a graviton). For the charged leaf of an electroscope to remain deflected, the constant microscopic work performed by gravitons in pushing the atoms of the leaf down has to be counteracted by the work of the massbound charges trapped in the leaves; this work, in turn, can only be sustained if the trapped charges draw in environmental latent heat to produce a flux of antigravitons sufficient to balance the constantly downward-pressing gravitational flux.
2. Mass-to-length transformation
Wilhelm Reich's experiments with the gravitational pendulum led him to postulate that atomic weights, specifically those of hydrogen, helium, and oxygen, can be functionally replaced by pendulum lengths. The Correas write: 'He never formally divulged the functional equivalence between mass and length. However, from careful analysis of the results of his pendulum experiments, one can enunciate the earth-shattering discovery of the equivalence between molecular mass and wavelength ...' The equation is: mass-equivalent wavelength (in metres) = molar mass (in grams) x 10-2.
The accepted molecular weight of the electron is 9.1094 x 10-28 g; multiplied by Avogadro's number this gives a molar mass of 5.4858 x 10-4 g, and a mass-equivalent (or gravitational) wavelength of 5.4858 x 10-6 m. If this wavelength has a physical meaning and is not merely an arbitrary number churned out by an arbitrary equation, it must be related in some way to both the structure of gravitons and the structure of the electron. But who has managed to crack the structure of the electron?
Orthodox physics has nothing meaningful to say on the subject as it does not offer a realistic physical theory of the subatomic world. In the standard model, 'fundamental' matter and force particles such as electrons, and hypothetical quarks and gravitons, are described as infinitesimal points, i.e. pure abstractions. String theory is claimed to advance our understanding of the quantum world, and even to be a giant step towards a 'theory of everything'. In reality, it dishes up further mathematical fantasies: it postulates that 'spacetime' is 10-dimensional, that the six additional spatial dimensions have conveniently undergone 'spontaneous compactification' and become unobservable, and that the fundamental constituents of matter are one-dimensional bits of wriggling and vibrating string, 10-33 cm long but with no width or thickness.
The latest fad is brane theory or M-theory, which postulates an 11-dimensional spacetime, inhabited not only by one-dimensional strings but also by two-dimensional membranes, three-dimensional 'blobs' (three-branes), up to and including nine-dimensional entities, not forgetting anti-branes and zero-branes. This is the sort of brainless claptrap that is nowadays passed off as 'science'!
Another example is the conventional interpretation of quantum physics, which claims that, when we are not trying to measure it, an electron, for example, is present in different places at the same time. It supposedly dissolves into 'probability waves', which magically 'collapse' into a localized particle again the next time a measurement is made. Louis de Broglie initiated an alternative interpretation, based on the notion that a subatomic particle is a real physical particle guided by a pilot wave - a theory further developed by David Bohm, Jean-Pierre Vigier, and others. The Correas have developed de Broglie's theory of matter waves in a different direction, linking it to specific wavefunctions and the notion of a dynamic, energetic, massfree aether.
Aetherometry proposes that all energy manifestations (mass-energy, kinetic energy, and the massfree energy of gravitons, latent heat or ambipolar radiation) always involve a primary superimposition between two wavefunctions, one internal and the other external to the associated linear momentum that defines the type of particle involved. If the energy manifestation is electric (e.g. electrokinetic energy or ambipolar energy), this primary superimposition couples an internal magnetic field wave with an external electric field wave (corresponding to the conventional function of electric potential). When generating massbound particles (through the process of secondary superimposition), aether wave energy is reconfigured into a circularized, looped flux.
This has led the Correas to develop a detailed toroidal model of the electron, which makes sense of various universally accepted, experimentally determined values. For instance, the looped flux forming the electron mass-energy is composed of a magnetic wave pursuing a circularized motion around the larger radius of the torus, and an electric wave pursuing a continuous helical motion around the smaller radius of the electron torus and wound around and transversely to the magnetic wave. The total flux path can be divided into 19,206 rings, a number equal to the reciprocal of the fine-structure constant squared (α-2). The circumference of each of these rings is equal to the Duane-Hunt wavelength (which the Correas extract from the Duane-Hunt law), and the total wavelength coiled around the torus therefore equals the mass-equivalent electron wavelength. The average of the two electron-torus radii is equal to the Bohr radius (the radius of the lowest-energy orbit in the Bohr model of the hydrogen atom).
3. Gravitational pendulums
In his pendulum experiments, Reich determined the value of pendulum length multiplied by the square of the frequency. He found that for pendulums with lengths of 1, 4, 16 and 64 cm, this number was an integer constant: KkrDS = 102,400 for double swings, or a number four times higher, KkrSS = 409,600, for single swings. These numbers are obtained by counting the number of swings per 64 seconds, which Reich called the 'org-minute'. Note that these four pendulum lengths are all powers of 4 (40, 41, 42, 43), and correspond numerically, by the mass-to-length transformation, to the atomic weights of hydrogen, helium, oxygen, and zinc respectively. Note also that 102,400 equals 45 x 102.
All these numbers belong to what Reich called the krx number series, where kr = 4. He considered this number system to be inscribed in nature. Pendulum lengths of 25 cm and 100 cm yield the same values of K. But for all other pendulum lengths, the product of length and frequency squared varies between 96,000 and 100,860. Reich therefore proposed that there are two classes of oscillatory pendulums and two classes of atomic elements: those with lengths or masses that belong to the krx number series and those that do not.
The 100 cm pendulum strikes seconds with each swing (180° pendular motion), while the 25 cm pendulum strikes seconds with each double swing (360° pendular oscillation). In other words, decreasing the pendulum length fourfold halves the oscillation frequency. For pendulums, the standard formula for gravitational acceleration is: g = 4π2l/T2. If the mean value of the gravitational acceleration at the Earth's surface is taken to be g = 9.81 m/s2, the accepted classical pendulum that strikes seconds with each swing needs to be 99.4 cm long. But Reich found that the pendulum which strikes seconds is 100 cm or 1 metre long, thus putting the general value of g at the Earth's surface at g = π2 = 9.8696 m/s2 (he called this pendulum the 'org-seconds' pendulum, since it yields the K constant when measurements are made using the org-minute).
Since angular frequency or velocity (ω) equals 2π/T (where T is the period of oscillation and ω is the frequency of oscillation in radians/sec), and since pendulum length (l) functions as a radius, we can also write: g = rω2. Thus, with the single and double swing constants now expressed in seconds:
gkrx = π2 m/s2 = 100π2 cm/s2 = 4π2l/T2 = rω2 = 4π2KkrDS = π2KkrSS
This novel treatment opens the way to understanding g as a circular function, or more specifically, as a function of cycloidal energy swings (see below); gkrx results from the synchronous action of π2 or about 10 single energy swings or wave impulses at the Earth's surface. How this can be reconciled with the fact that objects in free fall seem to fall vertically will be considered later. There is, of course, one clear similarity between pendulums and objects in free fall: just as gravitational pendulums depend for their beat solely on length and not on the suspended mass, so the time taken by an object in free fall to travel a certain distance is independent of its mass (d = ½gt2).
Clearly, Reich's value for g is slightly higher than the accepted value for gravitational acceleration at the Earth's surface. This is because his value corresponds to the gravitational field intensity E, and not to the net resultant acceleration, which varies with latitude:
E = GME / (RE + h)2 = GME / Ro2 = RoΩ2
where G is the gravitational constant, ME is the Earth's mass, RE is the Earth's mean radius, h is the altitude above the Earth's surface, Ro is the combined radius RE + h, and Ω is another angular velocity function that couples to Ro and is a constituent of the gravitational field intensity. Traditionally, this field intensity is considered to be counteracted by the centrifugal force created by the Earth's rotation; the centrifugal acceleration is zero at the poles and reaches a maximum of 0.03392 m/s2 at the equator. One of the problems in the current understanding of gravity is that the difference between the gravitational acceleration at the poles and at the equator is greater than any centrifugal reaction can account for. This discrepancy is conventionally explained by the Earth being not a perfect sphere but an oblate spheroid, or rather a triaxial spheroid.
Assuming that g = π2 m/s2, and taking account of the centrifugal reaction, the value of g at the equator should be 9.83568 m/s2, whereas the measured value is far lower: 9.780524 m/s2. How do the Correas explain the difference between these values? Their answer, which they intend to expand upon in future publications, is briefly as follows. Modern technology permits more exact determinations of the measured values of net g at the poles and the equator, along with better determinations of the polar and equatorial radii. This makes it possible to accurately determine the angular velocity function (Ω) that is a constituent of the gravitational field intensity. They point out that if we employ the values for net g at the poles (where no centrifugal reaction exists) along with the polar radii to determine the value of Ω, and then use this value together with the known equatorial radius to determine the gravitational field intensity at the equator, this will be found to be exactly π2 m/s2, to the fourth digit! This rules out geometric explanations for the actual value of net g at the equator, as the differences in terrestrial geometry are already taken into account. So something besides the centrifugal force or geometry must account for the counteraction of gravity at the equator by Δ = (π2 - 0.03392) - 9.780524 = 0.05516 m/s2. They contend that this antigravity effect is not due to geometry or uneven distributions of mass inside the Earth, but to a massfree energy effect whose nature they have not yet disclosed.
The classical foundation for the functional transformation of mass (m) into length (l) for the simple harmonic motion (SHM) of a pendulum is as follows:
- According to Hooke's law, the force exerted upon a point undergoing harmonic oscillation is: F = -kx, where k is a constant, and x is the displacement distance.
- Classical theory holds that if the displacement from the vertical is small, k = mg/l, where l is pendulum length.
- Angular frequency, ω = √(k/m).
- The period of simple harmonic motion, T = 2π/ω.
Hence:
T = 2π√(m/k) = 2π√[(m/(mg/l)] = 2π√(l/g)
We move on the left side of the expression from a mechanical relation that depends on inert mass, to a massfree relation where mass is replaced by pendulum length. The Correas also draw our attention to the fact that if we apply the mass-to-length transformation to k = mg/l, Hooke's constant (k) becomes functionally equivalent to the local gravitational acceleration constant (g).
4. Cycloids and gravity
In 1696 mathematician Jean Bernoulli offered a reward for the solution of the following problem: What shape is the curve on which a body subjected only to the force of gravity will slide (without friction) between two points in the least possible time? He and his brother Jacques, along with Leibniz, Newton, Huygens, and others, found the curve of fastest descent (or brachistochrone) to be part of an inverted cycloid, i.e. a curve generated by a point on the circumference of a circle that rolls along a straight line.
A trochoidal curve is one generated by a point anywhere on a straight line that passes through the centre of a rolling circle. For a cycloid (diagram A), this point (P) is located on the rim of the circle. The purple and red curves in diagram B are prolate and curtate cycloids respectively, the distance A-P1 being greater than the radius of the rolling circle, and A-P being shorter.
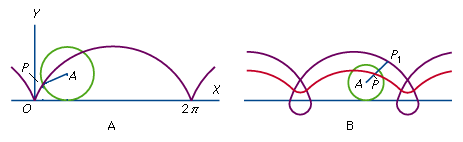
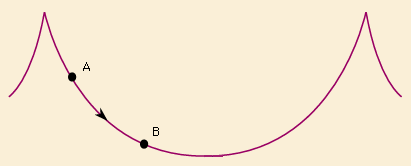
A swinging pendulum does not trace a perfectly circular arc but rather a cycloidal arc. The same applies to a park swing. Anyone who has played on one knows that when approaching 90° from the vertical, the chains visibly slacken. This is undoubtedly due in part to their weight, but it may also point to the cycloidal nature of the gravitational wave or 'massfree energy swing' that acts on the swinger or on pendulums. This is implied by the fact that, as Huygens demonstrated, in a gravitational field only the cycloidal curve is isochronous: the time taken by a particle to slide to the lowest point of an inverted cycloid is the same, no matter where on the cycloid the particle begins its descent. However, for a swinging pendulum, times of fall are only isochronous if the pendulum is released at an angle no greater than 57.5° from the vertical.
A rolling circle performs one revolution per cycloidal arch, or one cycloidal cycle. The linear length of the cycloid (LL) is equal to the circle's circumference (2πr), and the curved length (LC) - or the aetherometric wavelength of the cycloid - equals 4/π LL or 1.273 LL. The Correas contend that if it can be demonstrated that pendular length (l) for single swings directly converts into the wavelength of cycloidal motion, and still functions as the length equivalent of the inert mass of an element (i.e. m = lSS = LC), one should be able to crack the gravitational wavelength of elementary gravitons.
They argue that if a pendulum is released from the vertical, and the isochronous requirement is still to hold, the pendular swing will have to take the form of a gothic arch. The amplitude (i.e. the pendulum length) of the gothic arch (A''-C-A''') shown in the diagram below is 100 cm, the length of the org-seconds pendulum; the arc is generated by four synchronized rolling circles. The pendulum length is equal to the curvilinear length of the red cycloid and to four times its amplitude. Given that at 90°; to the vertical the pendulum length wraps itself around the cycloidal wave exactly, this wave becomes equivalent to the free massfree waveform of the pendulum length; every gravitational pendulum therefore has a specific wavefunction intrinsic to its swing.

As already mentioned, aetherometry proposes that all massfree energy units, including gravitational swings, consist of a primary superimposition of waves that is functionally equivalent to the superimposition of a particle or momentum with a wave. The wave (W1) intrinsic to the particle (or to the linear momentum carried by the massfree particle) is analogous in some respects to de Broglie's pilot or group wave, whereas the wave (W2) associated with the particle or extrinsic to momentum is analogous to de Broglie's phase wave.
In the case of gravitational energy, a single energy swing constitutes a full-cycle gravitational wave, and consists of an association of wave motion with the impulse or momentum connected with its forward linear motion. To put it another way, the massfree swing is composed of a particle (the aetherometric graviton) and its associated, extrinsic cycloidal wave. Since aetherometry claims that neutrons are decay particles, and that atoms are composed solely of two types of massbound particles - electrons/positrons and protons/antiprotons (or their families, which the Correas have identified in unpublished material) - there are only two fundamental kinds of gravitons: the electron-graviton class and the proton-graviton class. The gravitons of all known elements are composites of these two classes, and can be arranged in a Periodic Table of gravitons that parallels the Periodic Table of elements.
5. Mass-energy and gravitons
Energy has the conventional dimensions: m l2 t-2 (mass times length squared divided by time squared). By applying the mass-to-length transformation, this becomes: l3 t-2, denoting a volume of space synchronized with two resonant frequencies. In terms of fine structure, this corresponds to the product (superimposition) of a wavelength and two wavespeeds (λ W2), or to the product of a momentum and a wavespeed (p W), since momentum (= mass x velocity) has the aetherometric dimensions l-2 t-1 rather than the conventional dimensions m l t-1.
Aetherometry proposes that space is generated by, and in fact synonymous with, energy, rather than an empty nothingness that 'contains' energy. Massfree energy forms fluid lattices - composed not of a rigid, static grid of cells, but of energy events or fluxes which can interpenetrate and superimpose. When the fusion, or secondary superimposition, of two nonelectric aether energy units generates a massbound particle, an accompanying graviton is always formed as well. The massbound particle's 'gravitational mass' is equivalent to the wavelength of that quantum of graviton energy.
The master equation for the simplest matter-creation process is: aether energy unit squared (Eαn2) = mass-energy (Eδn) x graviton energy (EGn). A slightly more complex (cubic) superimposition of three aether energy units is shown to generate not only mass-energy and graviton energy, but also ambipolar radiation, which in turn produces the cosmic microwave background radiation (mCBR). So the mCBR is not the afterglow of some mythical 'big bang', in which all matter and energy, and even space and time, were created out of nothing, but the signature of the ongoing generation of matter out of the aether.
Each type of matter particle has its corresponding graviton unit. In addition to this gravitational energy quantum, there may be other gravitons attached to a grain of matter in accordance with the varying strength of local gravitational fields, for gravitons and antigravitons can also be created by the local aether lattice without the simultaneous creation of physical matter. A mass's weight is a gravitic force dependent on the average number of gravitational waves and associated momenta acting on it at any instant. In the case of the Earth, an object in free fall is subject to the repeating or pulsed action of almost 10 (π2) synchronous cycloidal waves or swings per second, which sequentially impart linear momentum and therefore kinetic energy to it.
The relation of an electron's mass-equivalent (or gravitational) wavelength to its torus structure was considered in section 2. Aetherometry proposes that the same wavelength functions as the wavelength of all the massfree energy swings (gravitons) which are constantly acting on the toroidal energy flux that constitutes the electron's inertial mass.
A body's gravitational 'mass' is therefore neither mass nor, strictly speaking, a property of that body per se, but rather the mass-equivalent wavelength of the graviton(s) anchored to and synchronized with the body's inert mass in any given local gravitational field. There is therefore no physical or energetic identity between inert mass and 'gravitational mass', as orthodox physics claims, but there is a functional and algebraic equivalence between the gravitational wavelength of a graviton and the inert mass it acts upon.
Every gravitational wavelength is a single-swing cycloidal wavelength. We saw above that a 100 cm pendulum strikes seconds with each swing, yielding a unit acceleration, KkrSS, equal to λ100f1002 or 1 m/s2. Aetherometry proposes that all gravitons share this acceleration constant, i.e. that the mass-equivalent wavelength (λn) of any particular grain of matter multiplied by its graviton frequency squared equals KkrSS. This means that graviton frequency is equal to the reciprocal of √λn, and its wavespeed is numerically equal to √λn. The gravitational waves accompanying an electron, for example, therefore travel very slowly through it: WGe = 2.342 x 10-3 m/s.
In the aetherometric model, gravitons and antigravitons do not move through space independently as such. They are anchored to massbound particles or to lattices of massfree and massbound charges, and move with them. Gravitons anchored to material particles are formed locally from the nonelectric aether, and last for the lifespan of the mass-energy or aether lattice to which they are attached, but during this time they are constantly being shed and regenerated, in the form of impulses from the local aether lattice that act upon the inertial mass of the associated massbound particle. What moves through space and is responsible for 'action at a distance' are aether lattices, carrying a certain number of 'free' gravitons (or antigravitons) anchored to them, and permitting the apparent propagation of gravity and gravitational disturbances through them. The apparent speed of propagation of gravity and gravitational disturbances through the aether is given by vG = c/WGe metre/sec = 1.2799 x 1011 m/s, or 426.95 times the speed of light.
6. Aether flux and celestial motions
Aetherometry proposes that the rotational and translatory movements of planets, stars and galaxies are the result of spinning (vortical) motions of massfree energy on multiple scales. Aether waves (associated with the influx of aether lattices) impart impulses to the Earth as they curve in towards the planet along cycloidal paths. This aether influx not only propels the Earth but also produces its gravitational field by 'pressing down' towards the planet's surface or centre. The aether vortex (with all its subvortices) that generates gravitational 'attraction' within the solar system can be pictured as a discoidal extension of the Sun.
Aether motion around the Earth can be deduced from satellite motion, since it is the motion of cycloidal massfree waves around a planet that sustains orbital motion. The translatory speed of a satellite is about 3 km/s 35,860 km above the Earth, increases steadily to 7.8 km/s at about 100 km, but decelerates abruptly at lower altitudes as a result of atmospheric and terrestrial absorption of the aether impulses, so that at tropospheric altitudes it would be no faster than the jet stream (0.01 to 0.1 km/s, relative to the Earth's equatorial spin velocity of 0.46 km/s).
The slightly faster west-to-east rotation of the aetherosphere compared with body Earth accounts for the results of Sagnac-type experiments conducted at the Earth's surface, which have shown that the speed of light is slightly faster around the Earth from east to west than from west to east. The almost vertical descent of most of the graviton flux at very low altitudes explains the apparent vertical motion of free fall. In reality, free fall is not vertical. First, an object in free fall partakes of the Earth's motions, including the local rotation velocity - the Earth's rotation being something that conventional physics is at a loss to explain. Second, the path of free fall is not even vertical or straight with respect to the rotating Earth, since the gravitational intensity varies locally on and above the surface of the Earth. An object in free fall actually travels through some segment of a cycloidal path, and is subject to the constant momentum imparted by locally formed gravitons released from the inflowing aether lattice, in a series of microscopic cycloidal swings or impulses, given that a semi-cycloid is the shortest-duration, frictionless (i.e. effectively massfree) slide path between two points.
The structure of aether lattices can be extracted from the fine or hidden structure of the universal constant G (see below). These lattices consist of nonelectric massfree energy in differential states of superimposition that generate cosmological leptons (their mass-energy), the lepton-gravitons that sustain these leptons, the massfree ambipolar radiation that electrically accelerates them and which they shed in the form of mCBR photons, and the lattice-seated 'travelling' gravitons (or antigravitons) that may also be shed. Aether lattices therefore contain interacting massbound and massfree charges, and comprise fluxes of gravitons and antigravitons. Gravitons impel a particle or body towards regions of greater mass density, and antigravitons impel it in the opposite direction, but the same massfree particle can function as either according to the net polarity of the underlying electrodynamic interaction between lattice charges. The planets are pushed both towards and away from the Sun through their dynamic gravitational/antigravitational interactions, resulting in a near steady state. The inflowing aether lattice streams responsible for terrestrial gravity have a dual origin, solar and galactic, and coincide with the fluxes of solar and galactic ambipolar radiation.
The aetherometric theory of gravity and the graviton differs in important respects from the conventional Le Sage impact theory of gravity. According to the latter, very tiny particles ('gravitons') are whizzing randomly through space in all directions, at some 20 billion times the speed of light, and the apparent 'attraction' between bodies is due to their shading one another from some graviton impacts. Aetherometry retains the gravity-as-push idea, but thinks in terms of massfree wave impulses acting on the elements of matter rather than solid particle collisions, and also introduces the idea of ordered lattice-seated graviton fluxes that account for celestial motions. Unlike most variants of Le Sage gravity, it also recognizes the existence of antigravity and the electrodynamic nature of gravitational forces.
7. Inertia and Newton's first law
Newton's first law of motion states that a body continues to move with a constant velocity or to remain at rest unless acted on by an external force. This law is fundamentally flawed: it assumes that for an object to preserve a state of motion (or rest) no work is required, no energy has to flow, and no force has to be deployed once a body has been set in motion. By contrast, aetherometry posits that no motion can be sustained without a flux of energy to replace the energy expended. Motion is always a function of energy, and even a state of relative rest is actually a state of circular energy flux. In other words, all is flux, motion, energy.
As we have seen, in the parallel field of electrostatics the Correas demonstrate that for an electroscope leaf to remain deflected, in a state of relative rest, an antigravitational force is required that permits conservation of a state of electric repulsion and of the electrokinetic energy of the massbound charges trapped in the stem and leaf. Linear motion at uniform velocity, too, requires energy transfer and energy expenditure. This is the fundamental omission in Newton's first law. The total power required to move a body at uniform velocity must increase with distance, and this requires a persistent external supply of energy even if there is looping of internal energy (as happens in the electrodynamic interaction of the charges trapped in the electroscopic leaf system).
In his commentary on the first law, Newton admitted that linear translatory motion will slow down even in a vacuum; in other words, conservation of inertia is imperfect and energy of motion will gradually be exhausted. He used the motion of the planets as an example of the conservation of uniform rectilinear translation, but this illustration is ill-chosen. For although the planets orbit the Sun with a constant mean velocity, planetary motion is curvilinear or angular, and therefore accelerated, given the continuous change in direction of the velocity vector, and is subject to constant fluctuations.
The Correas argue that there are no inertial, rectilinear motions; all motion is curvilinear and accelerated, and a constant mean velocity actually involves periodic accelerations and decelerations. All inertial systems are already accelerated ones. Uniform motion continues only for as long as the regular series of impulses sustaining it persists, and conservation of energy holds only for the system formed by the moving body and its environment, including the local massfree aether.
In newtonian physics, motion appears to occur in defiance of the law of conservation of energy, and is labelled 'inertial' to signify that it 'continues on its own'. Inertia is assumed to be a natural property of mass-energy and no further explanation is offered; indeed, no further explanation is possible, since orthodox physics has no realistic model of subatomic structures. The Correas argue that the inert mass of a grain of matter is a function of the characteristic wavelength of a quantity of massfree energy circularized into a torus as mass-energy. In line with an idea first put forward by Harold Aspden, they say that it is the tendency of massbound particles to try and conserve this energy (and thus their volume and internal structure) when accelerated that produces the property of inertia. In other words, inertia is a resistance by a quantity of mass-energy (and associated graviton energy) when it is accelerated by an externally imposed massfree field.
8. Centrifugal force and Newton's third law
Newton's first law deals with the inertia of a body moving at constant speed in a straight line. His third law requires an action to be balanced by an equal and opposite reaction, implying that the centripetal force of gravity should be balanced by a centrifugal force (an inertial force that obeys the second law, where force equals mass times acceleration), as is supposedly the case when describing stable satellite orbitals.
Free fall is clearly not counteracted by an equal centrifugal force, and it is one of the many instances in the real world when the third law fails. Free fall is counteracted only partially, and insufficiently in fact, by the centrifugal force developed by the Earth's rotation, whose magnitude depends on latitude. Centrifugal force is usually presented as a property of rotation, but its true source remains mysterious. The neo-Machian view is that centrifugal forces are inertial forces that ultimately arise from the gravitational attraction between the mass of a body and the rest of the mass in the universe.
The question arises as to why the third law is not broken at the critical height for a stable satellite orbit. Aetherometry suggests that a stable satellite does not in fact experience a centrifugal force equal and opposite in sign to the centripetal force of its weight. Instead, the orbital motion of satellites is sustained by the spinning aether flux enveloping the Earth. At lower altitudes the flux increasingly bends down towards the surface of the Earth, and loses transverse longitudinal velocity to gain near-vertical longitudinal velocity; gravitational acceleration (g) increases from 9.5 m/s2 at an altitude of about 100 km to about 9.8 m/s2 at the Earth's surface. But whereas the aether flux around the Earth results in satellites having a constant transverse speed, the velocity of a body in free fall steadily increases, because the body absorbs (and stores) more field energy from the local aether lattice than it expends through its free fall relative to the surface of the rotating Earth.
The Correas point out that just as classical and Lorentzian-relativistic electrodynamics ignore longitudinal electrical forces deployed along the direction of charge motion, so relativists ignore the longitudinal nature of the gravitational forces or swings responsible for both orbital motion and free fall. They further suggest that centrifugal forces are produced by rotating bodies because they arise as a function of weight transfer to the local aether lattice, i.e. as part of a primary gravitational interaction between a rotating body and the spinning local aether lattice.
9. Gravity and antigravity
Since force is traditionally defined as mass times acceleration, the conventional dimensions of force are m l t-2, i.e. mass multiplied by length divided by time squared (1 newton = 1 kg m s-2). Applying the mass-to-length transformation yields the aetherometric dimensions of force: l2 t-2. The gravitational force equation, F = Gm1m2/r2, implies that the gravitational constant (G) has the conventional dimensions l3 m-1 t-2. Aetherometrically, this becomes l2 t-2, i.e. the dimensions of force.
Aetherometry regards G as a universal force constant that results from a cosmic acceleration produced by the synchronous, ceaseless motion of massfree energy; in a very real sense, it is independent of matter and even of mass. A gravitational field is present everywhere in space, simply by virtue of the fact that space is produced by the activity of aether lattices. G is ultimately a function of the relation between electric and nonelectric massfree energy. This is underlined by one of the most basic exact functions for G discovered by Correas, where only the third term contains a massfree interaction, and the second includes the mass-energy (Eδe = mec2) of a cosmological electron and its associated graviton (EGe):
G = (h/2πmec2)2 vG (α m/s2)2 = (h2/4π2 EδeEGe) (vG-1 m/s) (α m/s2)2 = (h2/4π2 Eαe2) (vG-1 m/s) (α m/s2)2 = 1.10575 x 10-35 m2/s2
(Note that with CODATA's official values for fundamental units of measurement, the aetherometric determination gives 1.108 x 10-35 m2/s2.)
Another function for G expresses the intra-lattice interaction(s) as electrodynamic and involving both superimposition and differential relations between massfree and massbound charges; and still another expression accounts for the formation of lattice-seated gravitons, and involves quadratic superimposition of aether energy units (Eαe4). The Correas stress that these and other exact algebraic expressions for G always involve the coupling of established, fundamental physical values and functions with at least one genuine aetherometric quantity or function. They show that although the equation for G put forward by Sakharov (who regarded gravity as a zero-point-fluctuation force) yields the correct numerical value of G, it includes arbitrary and nonfunctional terms.
Primary gravity refers to a material body's gravitational interaction with the local aether lattice. The fundamental energy quantum of primary gravity is simply the product mG. So-called inertial forces - such as the centrifugal forces that arise from a body's rotation - transfer weight to a local lattice and take advantage of this primary gravitational interaction while appearing to be an antigravity effect.
Secondary (newtonian) gravity is a result of the forces that two or more bodies exert on one another through the aether, i.e. across lattices that connect them at a distance. The energy available to secondary gravity is the result of another phase superimposition of the separate energy quantities of primary gravity, Gm1 x Gm2, such that each body of a pair experiences an acceleration proportional to the distance between their centres of mass (gm2 = Gm1/r2 and gm1 = Gm2/r2), to yield a single force F = Gm1m2/r2. Hence, in contrast to the primary gravitational energy of a body or massbound particle, the energy of secondary gravity is given by Gm1m2/r.
In the final analysis, gravitational forces are essentially electrodynamic. Simplifying a bit, aetherometry contends that gravity ultimately results from an electrodynamic attraction that occurs when matter, which is mostly neutral or salt-like (with balanced charges of both polarities), interacts with aether lattices formed by in-phase ambipolar charges, whereas antigravity ultimately results from an electrodynamic repulsion that occurs when matter has net charge and interacts with the same in-phase ambipolar charge lattices. The Correas stress that genuine antigravity should be distinguished from weight cancellation or degravitation, from rotary transfer of weight to local lattices, and from levitational effects produced by electrostatic, electrodynamic, magnetostatic, and aerodynamic forces.
Eric Laithwaite demonstrated that Newton's third law is broken by force-precessed flywheels or gyroscopes, which appear to lose weight and generate little or no centrifugal force. The Correas agree with Harold Aspden that precession induces aether spin (or a local electric and vortical spin of the aether lattice), which decouples the inert mass of a flywheel from the flux of gravitons that normally give it weight. Furthermore, energy for translatory motion can be drawn from the rotary motion of interacting bodies, thereby producing out-of-balance linear forces that violate the third law.
As a result of their experimental and theoretical gravitational work, the Correas are in the process of developing two devices that cannot possibly exist according to accepted physics: a weight-neutralizer and an anti-gravitator. The weight-neutralizer is a tunable, target-directed device that can be used for short-range weight-cancellation of an object of known chemical composition. First-generation devices have a power consumption of a few watts, and can induce up to 100% weight loss in objects in the 100 mg range, by converting an ambipolar energy beam into antigraviton energy. Dr. Eugene Mallove witnessed demonstrations in which a piece of gold leaf was rapidly reduced in weight by 70% and 95% by imposing an ambipolar field with an electrical frequency adjusted to match that of the gold antigraviton.
The anti-gravitator develops the electroscopic kinetoregenerative phenomenon beyond weight neutralization to produce genuine negative gravity. According to a private communication from the Correas, this electrodynamic effect appears to be strictly monopolar, independent of ionization or ion-wind generation, independent of electrode geometry, and seated in the gravito-electrodynamic repulsion described above - as promoted by the interaction of monopolar lattices of massbound charges (responsible for the net charge of a body of matter) with in-phase ambipolar lattice charges. The Correas are highly critical of much of the experimental work that has been conducted on the 'Biefeld-Brown effect' - a force directed towards the smaller electrode of an asymmetric capacitor under a very high potential. Such experiments are often riddled with uncontrolled artefacts, have produced contradictory results, and confuse anomalies associated with electron emission and cathode reaction forces with antigravity. They argue that there is really no BB effect but that it is possible to generate a genuine electro-antigravitic force, or monopolar lift effect.
10. Correas vs. Spolter
In her book Gravitational Force of the Sun (Orb Publishing, 1993), Pari Spolter strongly criticizes the orthodox theory that gravity is proportional to the quantity or density of inert mass. It is well known that the gravitational acceleration of objects in free fall is independent of their mass. But Spolter goes as far as to argue that there is no reason to include any term for mass in either of the standard force equations (F = ma, and F = Gm1m2/r2). She rejects Newton's second law as an arbitrary definition or convention, and maintains that it is not force that is equal to mass times acceleration, but weight.
Her equation for 'linear force' is F = ad (acceleration times distance). Her equation for 'circular force' (including gravity) is F = aA, where a is acceleration and A is the area of a circle with a radius equal to the mean distance of the orbiting body from the central body. This equation implies that the acceleration due to gravity declines by the square of the distance, but that the gravitational force of the Sun, Earth, etc. is constant for any body revolving around it. In newtonian theory, by contrast, it varies according to both the mass of the orbiting body and its distance from the central body.
The Correas identify various flaws in Spolter's theory. Spolter does not question the equation for a body's momentum (momentum = mass times velocity), yet momentum with a rate of repetition constitutes a force, which therefore cannot be independent of mass. Moreover, weight is a type of force, rather than a distinct physical function. According to Spolter's newfangled definition of 'circular force', the gravitational force of a star or planet remains exactly the same no matter how far away from it we happen to be - such a conception of force seems counterintuitive if not absurd, and is unlikely to attract much of a following.
In Spolter's approach, 'linear' (one-dimensional) force and 'circular' (two-dimensional) force have different dimensions: m2s-2 for linear force, and m3s-2 for circular force. Similarly, 'linear' and 'circular' energy also have different dimensions, as they are calculated by multiplying linear or circular force by a body's 'critical mass'. The Correas argue that there is no justification for abandoning consistent definitions in this way: there are not two forms of energy, one linear and the other angular, one flat and the other volumetric. Specifically, they charge that Spolter confuses her 'circular force' with massfree energy. And if the mass-to-length transformation is applied to Spolter's equations, linear energy would have exactly the same dimensions as circular force (m3s-2)!
Using Spolter's equation, the gravitational force of the Sun would be 4.16 x 1020 m3s-2, a value that is constant for all planets, asteroids and artificial satellites orbiting it - no matter how far away they may be! The Correas point out that this value can also be arrived at by multiplying the length-equivalent mass of the Sun by the accepted value of G times π. But this value has the aetherometric dimensions of energy - not force. Moreover, this value does not describe the gravitational force of the Sun, nor a force acting at a distance upon any other body near to or far from the Sun; rather, after the π value is dropped, it comes close to describing the primary gravitational energy of the Sun.
Physically, gravity does not involve some (mean) area being accelerated around the Sun, as Spolter's equation implies. Rather, it involves a coupling of the mass-energy of the Sun and planets, along with their associated massfree gravitational energy. And gravitational forces act not through empty space but through the energetic aether - something that is as much missing from Spolter's physics as from orthodox physics.
Spolter claims that her gravitational equation solves the mystery of Kepler's third law of planetary motion. This law states that the ratio of the square of a planet's period of revolution (T) to the cube of its mean distance (r) from the Sun is always the same number (T2/r3 = constant). (Strictly speaking, Spolter's argument concerns the reciprocal of Kepler's constant [K-1 = r3/T2]). According to her equation, F = aA = (v2/r)(πr2). Replacing v with 2πr/T, gives: F = 22π3r3/T2; in other words, r3/T2 = constant, the 'constant' in question being equal to the 'gravitational force' of a particular star or planet divided by 22π3!
Thus, the value Spolter (wrongly) calls the gravitational 'force' of the Sun (4.16 x 1020 m3s-2) is equal to 22π3K-1. The Correas argue that this is a meaningless expression that obscures the real significance of Kepler's constant. They point out that Leibniz criticized Malebranche for a very similar confusion, when the latter thought that gravitational force was given by rv2 = 22π2K-1. If Spolter were right about 'circular force' and its energy-like dimensions, then all three Kepler radii (r3) should be fully circularized, and the expression should be 23π3K-1, or, alternatively, since Spolter thinks that gravity involves the acceleration of a mean area, two of the Kepler radii should be part of an area function (πr2), with the third being circularized (2πr), giving 2π2K-1.
Spolter's expression also differs from Newton's form of Kepler's third law, in which two radii are circularized: GM = 22π2K-1. This equation assumes that K-1 is equal to the inert mass of a celestial body multiplied by the gravitational constant divided by 4π2. It is impossible to place a star or planet on a balance and weigh it, and this is one of the methods used to determine their theoretical masses.
The Correas argue that to understand the true meaning of Kepler's constant and Newton's form of Kepler's third law, the latter has to be seen in relation to the entire solar system, as it is part of a function that defines the massfree energy of the primary gravitational interaction of the system as a whole. Aetherometrically, the correct relation is GMSS = 22π2K-1 (where MSS is the mass of the solar system), and the corresponding primary gravitational energy of each member of the system is a fraction of this, dependent on the ratio between its mass and that of the entire system. Hence, for the Sun: GMSun = (MSun/MSS) 22π2K-1.
Whereas conventional physics ignores the torque generated by the Sun's rotation, Spolter seeks to revive Kepler's theory and holds that the rotation of the primary body somehow generates its gravitational force, causing other bodies to revolve around it. But she does not suggest a mechanism to explain how this might work, or what causes a celestial body to rotate in the first place. According to aetherometry, it is the ordered inflowing aether fluxes that cause the planets and Sun to rotate, carry them forward in their respective orbits, and generate their gravitational fields.
11. Closing thoughts
Mainstream science labours under the delusion that it is steadily progressing towards a 'theory of everything' - a master equation concise enough to 'wear on your T-shirt', as one joker (a leading physicist) put it. In reality, physicists are plunging ever deeper into a morass of arbitrary and irrational mathematical fantasies. Infinitesimal particles, one-dimensional strings, multi-dimensional branes, collapsing probability waves, 10- or 11-dimensional spacetime, curved space, expanding space, spatialized time, dilated time, time reversal, backward causation, ex-nihilo creation - it seems that any garbage is acceptable as long as it avoids the need for a dynamic, energetic aether.
As Bertrand Russell once observed, 'What men really want is not knowledge but certainty.' Reigning paradigms do indeed offer scientists certainty and a sense of security, financial as much as intellectual, and this helps them to ignore, trivialize or suppress anomalies that expose the shortcomings of their cherished beliefs. Above all, official science has largely lost the willingness and ability to question, and sometimes even acknowledge, its own basic assumptions.
It is vital that alternative scientific models and viewpoints begin to receive a fairer hearing. Multiple working hypotheses and theories should be able to compete freely for attention and should be judged on their merits - on their grounding in experimental and observational facts, their ability to provide realistic explanations, to make accurate predictions, to generate new insights, and to spawn innovative technologies. On all these criteria, aetherometry scores very highly and therefore deserves careful scrutiny.
Acknowledgement
I would like to express my sincere thanks to Paulo and Alexandra Correa for reviewing this paper, and for open and frank discussion of all the questions raised.
Correas vs. Spolter: further debate