Akronos Publishing Concord, ON, Canada www.aetherometry.com

The aetherometric approach to solving the problem of magnetism

by Correa, Paulo N. & Correa, Alexandra N.

Published in January 2002.     30 pages.

Experimental Aetherometry, Vol. 2B

Monograph AS2-15

Price:   US $20   ($16 ISFA)

This monograph is also included in the print edition of Experimental Aetherometry, Vol. 2B

ABSTRACT Dimensional analysis of accepted fundamental functions of magnetic flux density B (Maxwell's 'magnetic induction') and magnetic field intensity H (Maxwell's 'magnetic force') exposes discrepant functions that are systematically inconsistent. In the cgs system, both B and H are treated as frequency functions, but in the SI or mks systems, B is shown to function as the reciprocal of a wavelength and H as an acceleration. The problem is further compounded by Maxwell's wrong dimensionality of current, by his admission of a variable dimensionality for the two fields in the electrostatic system of units, and the fact, uncovered by Aetherometry, that the field B relates to an angular length function, whereas H does not. These inconsistencies do not permit a correct understanding of what are the effective curls of H and B. To resolve the problem of magnetism means to solve for these H and B functions from first principles, seeking to make consistent both the functions and their dimensionalities. This is precisely the task of the present communication, which puts forth a comprehensive solution based upon the aetherometric treatment of J.J. Thomson's relation between balanced electric and magnetic forces. We begin by demonstrating how the gauss and the tesla, which are supposed to be equivalent measures of the magnetic field B in separate systems of units, are dimensionally inconsistent with each other. By employing aetherometric tools, we demonstrate how the gauss should actually be defined as - 1 gauss = 1 dyne/(esu * c) = 6.9065m-1 in compliance with the conventional and aetherometric definition of the tesla as: 1 tesla = 1 N m-1 amp-1 = 6.9065 *104 m-1 This leads us to directly extract the expression of the field B from the cyclotron frequency function Fcyclo, such that the value of B corresponding to a field of X gauss is given by: B = `X gauss' * * (2) Fcyclo)/c = X * 6.9065m-1 Once the Thomson relation for H and the electric field    is considered, the fine structure of magnetic wave functions can be elucidated, whether they apply to massfree charge, to the kinetic energy of massbound charge or to the mass- energy of charge carriers. 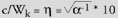The relation between the occluded frequency term of the gauss and the cyclotron frequency of the empirical gauss measured for electrons is shown to differ solely by the Eta-Correa constant: After differentiating between the H and B functions for massfree and massbound charges, we are led to conclude that whereas H-1 is the magnetic wavelength of massfree waves in "a vacuum", 2/B is the magnetic wavelength of the same waves in a "material medium". For electronic charges in a material medium, the magnetic wavelength is then simply a function of the radial magnetic vector r: 2B-1 = Wk/Fcyclo = 2r The findings suggest a totally new way of treating the magnetic permeability of a medium, and very different relations of the magnetic field functions to the current density terms Jfree and Jbound. These functions are systematized, for both massfree and massbound charges, and contrasted to those of Maxwell and accepted electromagnetic theory. Lastly, we demonstrate how the dimensionalities of H and B are the same, , even if one is the reciprocal of a radius and the other of a wavelength (composite or not), in contrast to the electric field    which is effectively a frequency function with dimensionality of t-1.